
Anyone who’s ever tried to play Magic: The Gathering or listened to a friend explain it to them has had to reckon with the learning curve of all its intricate rules and even more confounding cards. Human players might not be alone in feeling overwhelmed: A new research paper argues that the game is so complex that there are even cases where a computer theoretically wouldn’t be able to figure out how to win.
A group of researchers argues that Magic: The Gathering is so complex there are cases in which it would be impossible for a computer to figure out a fool-proof way to win. “This construction establishes that Magic: The Gathering is the most computationally complex real-world game known in the literature,” they write.
The team, which includes Alex Churchill, a board game designer, Stella Biderman, a researcher at the Georgia Institute of Technology, and Austin Herrick, a senior analyst at the University of Pennsylvania’s Wharton Budget Model initiative, wanted to see just how complex the fantasy card game was from a computational standpoint. What they ended up finding was that Magic: The Gathering isn’t just more complex than most other games, it’s actually noncomputable in some cases. It’s yet unclear just how many of those cases there are, but there are currently conceivable matches where there’s no way an algorithm can figure out the optimal path to victory.
The research was based on coding two decks of legacy Magic: The Gathering cards, which span the entire history of the game excluding certain banned cards, and creating a mathematical model to interpret the cards within the context of the game’s rules to return future board states based on which cards are played and in which order. As you can see from the following deck list, the cards used are some of the more complex ones from the game’s history.
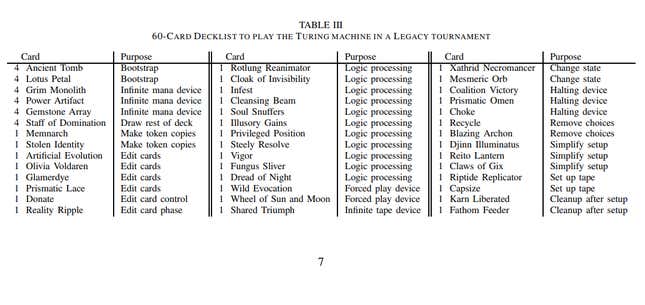
Cleansing Beam, for example, deals two damage to its target creature and each other creature that it shares a color with it. Coalition Victory, meanwhile, automatically lets you win the game if you control a land of each basic land type and a creature of each color. Then there’s Illusory Gains, an aura that automatically attaches to each new creature an opponent plays and brings it under your control. These card effects, combined with others, created enough alternative possible courses of action that the research team’s model was unable to return a result.
In chess it’s extremely resource intensive to compute how one side can win. After the first two moves in chess, there are 400 different possible outcomes. After the sixth, there are 121 million. It’s still theoretically possible to compute, though. Based on the noncomputable cases these researchers found, that’s not the case in Magic: The Gathering, despite the fact that it’s a two-player, zero-sum game using premade decks of cards, making it unique among all the other games currently studied in the field.
“This is the first result showing that there exists a real-world game for which determining the winning strategy is noncomputable,” the authors write.
Of course, this doesn’t apply to just any game of Magic: The Gathering. The researchers explored a very specific set of cards and starting hands based on certain requirements. For example, the decks “exclusively use cards with mandatory effects,” which means they don’t include cards where a player would choose from varied possible outcomes. But all of the cards used are tournament legal within the rules of the legacy format.
While the study has potential implications for game theory and computer science research, it also lays clear the sheer potential for discovery in Magic. “The full complexity of optimal strategic play remains an open question, as do many other computational aspects of Magic,” they authors write. “For example, a player appears to have infinitely many moves available to them from some board states of Magic…[which] has the potentially to highly impact the way we understand and model games as a form of computation.”
Ultimately it seems fitting for a game based in a multiverse whose rules are infinitely malleable.
[Update - 6:16, 5/8/19]: Shortly after publication, Alex Churchill, one of the authors of the paper, responded to Kotaku in an email with some further clarifications on the group’s findings.
“What we’ve proven is that the operation of “finding the best move in a game of Magic,” in the worst case, cannot be computed,” he said. “There are certain circumstances, even though they’re very contrived, where it’s proven that no algorithm can find whether there exists a winning move. In fact, since we eliminate all player choice, we’ve proved something slightly stronger: that it’s impossible in the general case for an algorithm to look at a board state and see whether it’s possible for the game to end at all.”
He went on:
“This is what computer scientists care about when they talk about the complexity of an algorithm. The algorithm might be easy to solve in almost all cases, but we’ve shown that the worst case is as hard as it can be.”
“This has very little implication for playing the game in practice, but it does have takeaways for potential AI designers. Probably anyone who was going to write an AI for Magic would not have made the AI choose its next move by trying to exhaustively compute all possible consequences of the current board state - that’d be crazy. They’d do it using heuristics, rules of thumb that give a best guess about how to play. Our paper just proves that the exhaustive computation approach is definitely not the way to go because it’s actually impossible (in some cases).”